Definition

In the setting of principal bundle morphism, a reduction of the structure group of a principal bundle $P(G, \pi, B)$ over a base space $B$ with structure group $G$ is what follows. Suppose $H$ is a subgroup of $G$, and let $h: H \rightarrow G$ denote the inclusion map. A reduction of the structure group from $G$ to $H$ refers to the existence of a principal $H$-bundle $P'(H, \pi', B)$ and a principal bundle morphism $f: P' \rightarrow P$, $f=(f_P,id)$, i.e.:

1. The diagram

commutes, meaning $\pi \circ f_{P} = \pi'$.

2. The $H$-equivariance condition for $f_{P}$ is satisfied:

where $h(g) = g$ as $H$ is a subgroup of $G$.

Extension and restriction of a

Definition

([Schuller 2013] page 178. There are some gaps in the definition and in the theorem, I think. On the other hand, I think this can be also calle group reduction or group structure reduction.)

Let $H$ be a closed subgroup of $G$. Let $(P,\pi, M)$ a principal $G$-bundle and $(Q,\pi',M)$ a principal $H$-bundle. If there exists a principal bundle morphism $u$ from $P$ to $Q$, i.e. a smooth bundle map which is equivariant with respect to the inclusion $H \subseteq G$ then $Q$ is called an $H$-restriction of $P$ and $P$ is called a $G$-extension of $Q$.

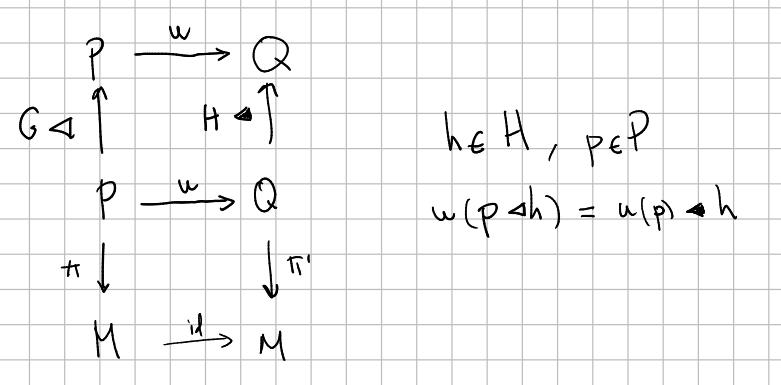
Theorem

[Schuller 2013] page 178.

Let $H$ be a closed Lie subgroup of $G$.

i) Any principal $H$-bundle can be extended to a principal $G$-bundle.

ii) A principal $G$-bundle $(P,\pi, M)$ can be restricted to a principal $H$-bundle if and only if the bundle $(P/H,\pi',M)$ has a section.

Proof

I don't know.

Idea of ii). Think of the orthonormal frame bundle. Also, see G-structure .

Particular cases

• The orthonormal frame bundle.

• When the principal bundle is the frame bundle we have G-structures.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es